数形结合的思想方法在问题解决中的应用
南溪区钟灵街小学 谢清洪
小学是学生学习数学知识的启蒙时期，这一阶段注意给学生渗透基本的数学思想显得尤为重要。数形结合思想对研究和应用数学具有指导意义，学生一旦掌握将会终身受益。
数形结合思想是小学数学教材编排的重要原则，也是小学数学教学的一个重要特点，更是解决问题中常用的方法。特别对于小学数学教学的重难点之一----应用题教学来说，针对小学生年龄小、认知能力简单、抽象思维能力弱的实际，充分渗透数形结合思想，把应用题中的数量关系用最恰当、最清晰的图形表示出来，化抽象为直观、化繁杂为简单、化隐含为显见，可有效地激发小学生学习数学的兴趣和积极性，提高其分析问题和解决问题的能力，同时也进一步拓展应用题教学的方式方法，常能收到事半功倍的效果。
数形结合就是通过数(数量关系)与形（空间形式）的相互转化、互相利用来解决数学问题的一种思想方法。它既是一个重要的数学思想，又是一种常用的数学方法。数形结合，可将抽象的数学语言与直观的图形相结合，是抽象思维与形象思维结合。有些数量关系，借助于图形的性质，可以使抽象的概念和关系直观化、形象化、简单化；而图形的一些性质，借助于数量的计量和分析，得以严谨化。那么在小学数学解决问题教学中如何利用数形结合的思想呢？以下根据自身的数学教学实践谈谈自己的粗浅见解。
一、数形结合的思想在解决图形的面积问题中的应用
著名教育家皮亚杰说过：“儿童是具有主动性的人，所教的东西要能引起儿童的兴趣，符合他们的需要，才能有效地促使他的发展。”比如，在三年级下册教学长方形的面积时，有这样一道练习题：有一块长方形菜地，它较长的一条边靠着墙，长20米，用篱笆将这个菜地围起来要40米。这个菜地的面积是多少平方米？
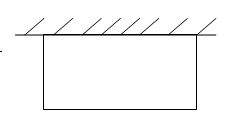我们在解决这样的问题是，该如何引导学生去解决呢？仅从题上文字去看，有两个数据，知道长20米，篱笆有40米，但怎样去围呢？学生在头脑中没有多大印象。首先，我们可以假设我们的教室是一块菜地，让学生亲身去围一围，体验一下长方形菜地的生活模型，当学生有了对长方形菜地的初步认识后，再让学生去画一画这块长方形菜地，通过画图，哦，学生突然发现，原来长方形菜地是样围成的。40米的篱笆只围3条边就可以了（如下图）。知道长边是20米，那短边就是
（40-20）÷2=10（米）这样算出的长方形菜地的面积是：20×10=200（平方米）
二、数形结合的思想在解决行程问题中的应用
陶行知先生说过：“创造始于问题”。学生没将题目读懂时，他是没有问题的，这与他没读题效果一样。只有钻研之后，才会生出“看似绝壁，却辟小径”之感。比如，我们在教学行程问题时有这样一道题：天津到济南的铁路长357千米。一列快车从天津开出，同时有一列慢车从济南开出，两车相向而行，经过３小时相遇，快车平均每小时行79千米，慢车平均每小时多少千米？
首先，我们要求学生读懂题意，鼓励多提问。教师把可能出现的问题都要预设清楚：题目意思是什么？哪两位同学上讲台来表演快慢车的相遇？你们撞上了，车能撞吗？在中间相遇吗？能用图形表示吗？除了用线段图，长方形图，还能用圆柱形的，轨道形的吗？它们的数量关系是什么？你用哪种数量关系解题？还有其它方法吗？可能出现什么错误？怎么改？其次，学生围绕着问题与图形，反复在数与形之间辗转，借直观，解抽象，把一个无从下手的题目具体化。通过汇报，有多种解法，可列出学生容易理解的几种式子，再结合直观图，比较最简单的一种解题思路。最后，学生在老师的引领下，领悟“数形结合”的数学思想。充分利用图形的直观性和具体性，发现数量关系，找出解决问题的突破口。画图不仅是为了解题，更为重要的是建立图文并茂的场景图，让孩子们的思维体操更准确，更潇洒。
三、数形结合的思想在解决和倍、差倍问题中的应用
和倍问题是已知大小两个数的和与它们的倍数关系，求大小两个数的应用题.为了帮助我们理解题意，弄清两种量彼此间的关系，常采用画线段图的方法来表示两种量间的这种关系，以便于找到解题的途径。
比如有这样一道题：
甲班和乙班共有图书160本。甲班的图书本数是乙班的3倍，甲班和乙班各有图书多少本？首先，我们应根据题意画出线段图（如图所示）、
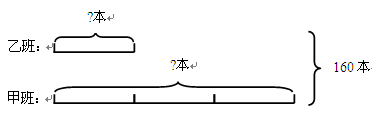
解析：乙班：160÷（3+1）=40(本) 甲班：40×3=120(本)
前面讲了应用线段图分析“和倍”应用题，这种方法使分析的问题具体、形象，使我们能比较顺利地解答此类应用题.下面我们再来研究与“和倍”问题有相似之处的“差倍”应用题。“差倍问题”就是已知两个数的差和它们的倍数关系，求这两个数。差倍问题的解题思路与和倍问题一样，先要在题目中找到1倍量，再画图确定解题方法.被除数的数量和除数的倍数关系要相对应，相除后得到的结果是一倍量，然后求出另一个数，最后再写出验算和答题。比如：
光明小学开展冬季体育比赛，参加跳绳比赛的人数是踺子人数的3倍，比踢踺子的多36人。参加跳绳和踢踺子比赛的各有多少人？
解析：36÷（3－1）=18（人） 18×3=54（人）
四、数形结合的思想在解决植树问题中的应用
学习“植树问题”时，先与学生们一起玩手指游戏。即出示两个手指，让学生观察，有几个手指几个间隔？“两个手指一个间隔。”接着出示三个手指，让学生观察，有几个手指几个间隔？“三个手指两个间隔。”……从而得出手指数和间隔数之间的关系是：手指数＝间隔数＋1。学生通过建立手指和间隔数之间的关系后，接着情境引入，出示例题：“同学们要在长30米的小路一边植树，每隔5米种一棵，两端也要种。一共需要多少棵树苗？”然后让学生分组讨论，根据自己的理解列式解答，并设法验证。汇报时，有些学生是通过画示意图，进行“实地”植树来验证；更多的学生是通过画线段图来说明。大家均验证出：在两端都种的情况下，植树的总棵数＝间隔数＋1，像这样，把算式形象化，学生看到算式就联想到图形，看到图形能联想到算式，更加有效地理解了植树问题的算理。
五、数形结合的思想在解决鸡兔同笼的问题中的应用
心理学研究表明，儿童接受具体性文字中的信息比学习抽象性文字中的信息容易得多，其原因是由于具体名词能产生心理映像，而儿童利用形象的图式学习比用纯文字推演更有兴趣、更容易学习。但另一方面，用数学符号和专用术语呈现的数学，由于其严谨、清晰、简约、深刻，更体现着数学学科在培养儿童的科学精神中的真正优势。
鸡兔同笼问题，也是从图形中总结出解决方法。如：鸡和兔一共有8只，腿有24条。求鸡和兔各有多少只？ 用算术方法解决鸡兔同笼问题，有的学生不能完全理解，而借助画图，一步一步总结方法和规律，帮助学生理解。先画8个圆，表示8只动物，假设全是鸡，给每个圆画2条腿。共画了16条腿。还有24-16=8（条）没有画上，再把剩下的腿添上，每个圆还可以添2条，8条腿可以添8÷2=4（只）。从画好的图中可以看出，这4只动物有4条腿，是兔。只有2条腿的有4只，是鸡。
综上所述，“形”和“数”是数学知识表现的两种形式，“数”准确而抽象、“形”形象而粗略，各有所长。而数形结合是一种极富数学特点的信息转换方式，这种转换不仅有助于数学的多样化表现，也有利于儿童更好地认识数学——用数量的抽象性质来说明形象的事实，同时又用图形的性质来说明数量的抽象性质，这正是数形结合的本质所在。
在小学数学教学中,数形结合思想是数学解题中常用的一种思想方法,在数学问题中若能“以数示形,以形思数,数形渗透”,则能加强知识的横纵联系.数学是研究客观世界的空间形式和数量关系的科学,数是形的抽象概括,形是数的直观表现.华罗庚教授曾说：“数缺形时少直觉,形少数时难入微.数形结合百般好,隔裂分家万事非.”数形结合的思想就是充分运用数的严谨和形的直观,将抽象的数学语言与直观的图形语言结合起来,使抽象思维和形象思维结合,数形结合是小学数学新课程所渗透的重要思想方法之一,相关教材中的内容能很好地培养和发展学生的数形结合思想.教材中这一方法的渗透对发展学生的解题思路、寻找最佳解题方法有着指导性的作用,可对问题进行正确的分析、比较、合理联想,逐步形成正确的解题观,还可在学习中引导学生对抽象概念给予形象化的理解和记忆,提高数学认知能力,并提升对现实世界的认识能力，从而提高数学素养,不断完善自己。
