数形结合的思想方法在解决问题中的应用
四川省宜宾市屏山县学苑街小学:罗萍
华罗庚先生说过:“数缺形时少直观,形少数时难入微,数形结合百般好,隔裂分家万事休。”的确,数形结合的思想方法能将抽象的数学语言与直观的图像相结合起来,把复杂的问题简单化,抽象的问题形象化,因此,教师应将“数形结合”的思想贯穿于数学教学的始终,学生在解决问题时才能真正做到以形助数、以数解形、数形互换,从而优化学生解决问题的途径,提高学生解决问题的能力,以实现学生数学素养的整体提高。
一、 以形助数,有利于学生理解数学问题的本质。
小学生的思维是以形象思维为主,学生对抽象的数学问题的理解比较困难,而以形助数能将抽象的问题具体化、形象化,便于学生理解数学问题的本质,提高学生解决问题的能力。例如:在教学每个花瓶插5朵花,6个花瓶能插多少朵花时,学生不能理解求6个花瓶能插多少朵花究竟是求6个5是多少,还是求5个6是多少时,我就引导学生用圆形代替花朵,动手画一画,(如图所示:○○○○○ ○○○○○ ○○○○○ ○○○○○ ○○○○○ ○○○○○)然后再让学生动手数一数,通过画一画、数一数学生明白了这道题是求6个5是多少,根据乘法的意义迅速列出了算式,解决了问题。又如:在教学把一根绳子对折两次后,每段长8米,这根绳子长多少米时,学生拿着题无从下手,根本不能理解题意,于是我找来一根绳子演示什么叫对折,让学生在直观演示中理解对折,观察对折1次后绳子变成了几段,再让学生继续观察再次对折后绳子变成了几段。通过直观演示将数转化为形,学生深刻理解了问题的本质,抓住了解决问题的核心,困难就引刃而解了。可见以形助数能帮助学生理解问题的本质,抓住解决问题的核心,提高学生解决问题的能力。
二、 以数解形,能拓宽学生解决问题的思路。
图形虽然直观、形象,但是缺少了数就不能揭示图形的本质属性和图形所蕴含的的数量关系。因此以数解形不但能拓宽学生的解题思路,提高学生解决问题的能力,而且还能促进学生的创新思维的发展和学生数学素养的提高。例如:在教学了用厘米作单位量长度后,让学生分别测量长方形和正方形4条边的长,看看能发现什么?学生一边测量,一边在每条边上标出数据,然后对测量的数据进行观察、比较、分析,小结得出长方形对边相等,正方形4条边相等的结论。学生结合对线段的测量,不但了解了图形的某些性质可以用数来描述,而且在解决问题的过程中思路也得了到拓宽。又比如:在教学角的各部分名称时,教师先出示不同类型的角,让学生仔细观察,找出这些角的共同特征,学生通过看一看、找一找、议一议很快发现这些角都有1个顶点,2条直直的边,就这样学生从数的角度来描述了这些角的共同特征,揭示了角的三大要素,提高了自身解决问题的能力,促进了自身创新思维的发展。再比如在教学中为了帮助学生进一步理解角的本质属性,教师出示了下图,让学生辨析它们是不是角,学生通
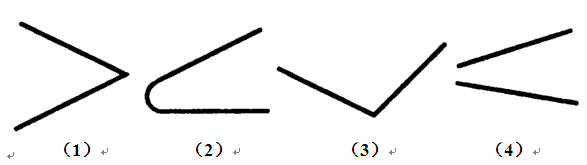
过观察、思考迅速作出了判断,(1)、(3)是角,因为它们都有1个顶点,2条直直的边;(2)、(4)不是角,因为图(2)不止1个顶点,图(4)没有1个共同的顶点,学生用数字揭示了角的本质属性。可见以数解形能拓宽学生的解题思路,促进学生的创新思维的发展和素质的整体提高。
一、 数形互换,能优化解决问题的途径。
数和形的结合实质上就是形象思维和抽象思维的结合,在解决问题时既要借助“形”的生动和直观性认识“数”,又要借助于“数”来精确和规范地阐明“形”的属性。即通过形感知数,通过数认知形。所以数形互换不但能让学生学会从不同的角度去思考问题,创造性地解决问题,而且还能让学生在解决问题的过程中自觉地优化解题途径,提高解决问题的效率。例如:教学倍的认识时,让学生在第一行摆3根小棒,第二行摆6根小棒,3根3根地摆,待学生操作完毕,教师追问6里面有几个3?学生根据操作迅速作答6里面有2个3,此时教师再告知学生6里面有2个3,我们就说第二行小棒的根数是第一行的2倍。让学生借助小棒的直观形象初步感知了倍的意义,同时也让学生明白了用数阐述两行小棒之间的关系更精确、更简洁。为了进一步让学生深刻理解“倍”的含义,教师又出示10朵红花和2朵黄花图,让学生2朵2朵地圈红花,通过圈一圈,学生发现10里面有5个2,红花的朵数就是黄花的5倍,学生用数准确地描述了红花与黄花朵数之间的关系,进一步地理解倍的含义。接下来教师再让学生议一议8里面有几个4?8是4的几倍?并鼓励学生用不同的方法来解决这两个问题,通过议一议、想一想,有的学生在全班交流时说:我在脑子里想小棒图,左边摆了4根小棒,右边摆了4根小棒,合起来是8根小棒,所以8里面有2个4,8是4的2倍。也有的学生交流说:我用的是乘法口诀,因为二四得八,所以8里面有2个4,8是4的2倍。还有的学生交流说:因为8÷4=2,所以8里面有2个4,8是4的2倍。就这样学生在见形想数,见数思形,用“数”去研究“形”的过程中学会了从不同角度去思考问题,拓宽了学生解决问题的思路,并在解决问题的过程中自觉地优化了解题途径,提高了学生解决问题的效率,收到了事半功倍的效果。
总之,“数形结合”既是一种解决问题的方法,又是一种重要的数学思想,教师在数学教学中应该坚持不懈的渗透数形结合的思想方法,让数形结合的思想方法在学生的头脑中生根发芽,成为学生解决问题的重要途径,从而促进学生解决问题的能力和数学素养的全面提高。