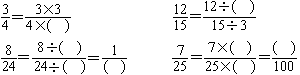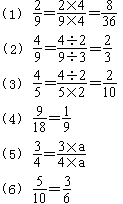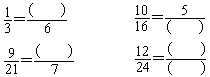毛小学 翁叶卫

【 教学目标 】

亲历分数基本性质的形成过程，掌握分数的基本性质及意义。

能运用分数的基本性质把分数化成既约分数（分子和分母是互素的分数）

经历观察、操作、合作等学习活动，感受数学与生活的联系及学习数学的乐趣。

【 教学重点 】

亲历分数基本性质的形成过程，掌握分数的基本性质

能运用分数的基本性质把分数化成既约分数（分子和分母是互素的分数）

【教学难点】

1、引导学生亲历分数基本性质的形成过程

【 教学过程 】

一、故事引人，揭示课题

1．教师讲故事：孙悟空巧戏猪八戒

有一天，素呢和猪八戒在分饼吃，孙悟空说我们把它平均分成 2份，每人1份怎么样？猪八戒说：“不行，1份太少了，我吃不饱！”“那咱们就把它平均分成4份，每人2份吧！：”猪八戒耷拉着脑袋说：“还是不行。”孙悟空故意叹了口气：“那就平均分成8份，每人4份总行了吧！” “那还差不多！”猪八戒背起耙子乐呵呵地笑了。

2、请同学们思考一下：猪八戒和孙悟空谁聪明？为什么？

猴山上的猴子最喜欢吃猴王做的饼了。有一天，猴王做了三块大小一样的饼分给小猴们吃，它先把第一块饼平均切成四块，分给猴 1一块。猴2见到说：“太少了，我要两块。”猴王就把第二块饼平均切成八块，分给猴2两块。猴3更贪，它抢着说：“我要三块，我要三块。”于是，猴王又把第三块饼平均切成十二块，分给猴3三块。小朋友，你知道哪只猴子分得多吗？

讨论：哪只猴子分得的多？学生发表自己的意见。

教师出示三块大小一样的饼，通过师生分饼、观察和验证，得出结论：三只猴子分得的饼一样多。

引导：聪明的猴王是用什么办法来满足小猴子们的要求，又分得那么公平的呢？同学们想知道吗？学习了“分数的基本性质”就清楚了。（板书课题）

[一上课，先听一段故事，学生非常乐意，并会立即被吸引。思考故事当中提出的问题，学生自然兴趣浓厚。通过故事设疑，激起了学生探求新知的欲望。]

2．组织讨论。

（ 1）既然三只猴子分得的饼同样多，那么表示它们分得饼的分数是什么关系呢？这三个分数什么变了，什么没有变？让学生小组讨论后答出：这三个分数是相等关系， ＝ ＝ ，它们平均分的份数和表示的份数也就是分数的分子和分母变化了，但分数的大小不变。

（ 2）猴王把三块大小一样的饼分给小猴子一部分后，剩下的部分大小相等吗？你还能说出一组相等的分数吗？通过观察演示得出： ＝ ＝ 。

（ 3）我们班有40名同学，分成了四组，每组10人。那么第一、二组学生的人数占全班学生人数的几分之几？引导学生用不同的分数表示，然后得出： ＝ ＝ 。

3．引入新课：黑板上三组相等的分数有什么共同的特点？学生回答后板书：

分数的分子和分母变化了， 分数的大小不变。

它们各是按照什么规律变化的呢？我们今天就来共同研究这个变化规律。

二、比较归纳，揭示规律

1．出示思考题。

比较每组分数的分子和分母：

（ 1）从左往右看，是按照什么规律变化的？

（ 2）从右往左看，又是按照什么规律变化的？

让学生带着上面的思考题，看一看，想一想，议一议，再翻开教科书看看书上是怎么说的。

2．集体讨论，归纳性质。

（ 1）从左往右看，由 到 ，分子、分母是怎么变化的？引导学生回答出：把 的分子、分母都乘以2，就得到 。原来把单位“1”平均分成4份，表示这样的3份，现在把分的份数和表示份数都扩大2倍，就得到 。

板书：

（ 2） 是怎样变化成 的呢？ 怎么填？学生回答后填空。

（ 3）引导口述： 的分子、分母都乘以2，得到 ，分数的大小不变。

（ 4）在其它几组分数中，分子、分母的变化规律怎样？几名学生回答后，要求学生试着归纳变化规律：分数的分子和分母都乘以相同的数，分数的大小不变。

（板书： 都乘以 相同的数 ）

（ 5）从右往左看，分数的分子和分母又是按照什么规律变化的？通过分析比较每组分数的分子和分母，得出：分数的分子和分母都除以相同的数，分数的大小不变。

（板书： 都除以 ）

（ 6）引导思考：都乘以、都除以两个“都”字，去掉一个怎么改？（去掉第二个“都”字，换成“或者”）再对照教科书中的分数基本性质，让学生说出少了什么？（少了“零除外”）讨论：为什么性质中要规定“零除外”？

（板书： 零除外 ）

（ 7）齐读分数的基本性质。先让学生找出性质中关键的字、词，如“都”、“相同的数”、“零除外”等。然后要求关键的字词要重读。师生共同读出黑板上板书的分数基本性质。

[新知识力求让学生主动探索，逐步获取。“猴王分饼”和分析班级学生人数得出的三组相等的分数为学生探索新知提供材料，出示的思考题是学生探求新知、独立思考的指南，教师环环紧扣的提问以及引导学生逐步展开的充分的讨论，帮助学生一步步得出结论。]

3．出示例2：把 和 化成分母是12而大小不变的分数。

思考：要把 和 化成分母是12而大小不变的分数，分子、分母怎么变化？变化的依据是什么？

4．讨论：猴王运用什么规律来分饼的？如果小猴子要四块，猴王怎么分才公平呢？如果要五块呢？

[得出性质后，再让学生说出猴王的想法，并回答如果小猴子要四块，猴王怎么办？既前后照应，又让学生在帮猴王想办法的过程中，运用新知解决实际问题。]

5．质疑：让学生看看课本和板书，回顾刚才学习的过程，提出疑问和见解，师生答疑。

三、沟通说明，揭示联系

通过举例，沟通分数的基本性质与商不变性质之间的联系。引导学生运用分数与除数的关系，以及整数除法中商不变的性质，说明分数的基本性质。

如： ＝3÷4＝（3×3）÷（4×3）＝9÷12＝

[学生运用分数与除法的关系，以及整数除法中商不变性质说明分数的基本性质，实现了新知化归旧知。]

四、多层练习，巩固深化

1．口答。

学生口答后，要求说出是怎样想的？

2．判断对错，并说明理由。

运用反馈片判断，错的要求说明与分数的基本性质中哪几个字不相符。

3．在下面（）内填上合适的数字。

采取师生对出数的游戏形式进行，如先由教师出分子，再让学生对出分母，也可以先由学生出分母，再让教师对出分子。

4．连续写出多个相等的分数。比一比，在1分钟内看谁写得多。

让写出相等分数最多的学生报出来，师生予以表扬鼓励。

5． ＝ （a、b是自然数），当a＝1，2，3，4……时，b分别等于几？

讨论： a与b之间的关系是怎样的？为什么会存在这样的关系？依据是什么？

6．把 、 、 、 和 化成分母相同而大小不变的分数。

思考：分数的分母相同了，有什么作用？揭示学习分数的基本性质的重要性，鼓励学生学好、用好。

7．圈分数游戏：圈出与 、 相等的分数。

让学生拿出写有若干个分数的练习纸，圈出与 、 相等的分数。然后，教师在投影仪上，用叠片框出学生圈出的数，屏幕显示出“星星火炬”的图案，表扬学生为“星星火炬”增添了新的光彩。

[练习设计由易到难，由浅入深，既巩固新知，又发展思维，其间还自然地渗透思想品德教育。师生相互出数做题，能够创设民主和谐的学习气氛。揭示 ＝ （a、b自然数）中a与b的倍数关系，巩固了新知，通过举例，还渗透了函数思想。]

五、课堂小结

六、课堂作业

教科书练习二十三第 4、5题。

七、动脑筋出教室游戏

 让学生拿出课前发的写有分数的纸片，要求学生看清手中的分数。与 相等的，报出自已的分数后先离场，与 相等的再离场，与 相等的最后离场。