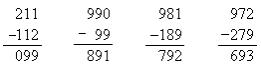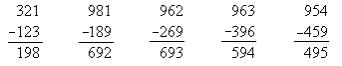我刚才说我找到二位数学世界的“黑洞”，很自然地，我就想是否在三位数的世界也有“黑洞”存在？于是我又开始我的旅行了。

我住的房子是107号，于是我就想像我要从“107号星球”到另外一个星球去。我将｛1，0，7｝先根据大到小的排法，得到的三位数，减掉由小到大的排法所组成的数，也就是710-017=693。

我的下一个星球就是由｛6，9，3｝根据从大到小的排法所组成的数，即963。

于是我画一个箭头“→”，写成 107→963。

从963我算到：963-369=594。

于是我有107→963→954。

由954我得到：954-459=495。

因此根据我以上的走法，我又回到954了，即：

107→963→954

我想到《广角镜》的地址是在184号，于是我在第二次就由“184号星球”出发：

841-148=693

奇怪！我有：184→963→954

我的好朋友老牟住在118号，于是我就算：

因此我有 118→963→954

常与我通讯的小黄弟弟是住在121号。我就算：

我得到121→990→981→972→963→954

能说善道又颇有文才的老董是住在606号。于是由此我得：

606→954

从事电子计算机研究工作的周大姐，她的工作地址是251号，于是我计算得到：

251→963→954

真是奇妙！我从不同的星球出发最后都要落进954去。这是偶然现象，还是必然现象呢？我只试了6个星球，而在三位数世界里却有几百个星球，是否每个星球都会最后落进954去呢？或许会有例外的情形，我还没有发现到呢？

我就再拿一个数来试验，很自然地我想到是123，

用我以上的写法我得到：

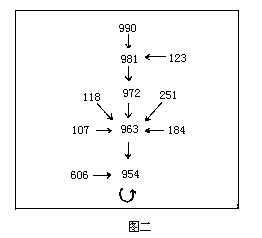
123→981→962→963→954

我画了下面的图二（见下页）：

图二中的954是否三位数世界的“黑洞”？

于是我就大胆地作下面的猜想（conjecture）：“954是三位数世界里的‘黑洞’，只要从任何个十百位数不会全部一样像111，222，888的三位数出发，它们一定最后掉进954里而不会出来。”