VCM主题资源

例1、例2	体验事件发生的确定性和不确定性。
例3、例4、例5及相关内容	能够列出简单试验所有可能发生的结果，知道事件发生的可能性是有大小的。

对于纷繁的自然现象与社会现象，如果从结果能否预知的角度出发去划分，可以分为两大类：一类现象的结果总是确定的，即在一定的条件下，它所出现的结果是可以预知的，这类现象称为确定现象。例如，抛一个石块，可预知它必然要下落；在标准大气压下且温度低于0℃时，可预知冰不可能融化。另一类现象的结果是无法预知的，即在一定的条件下，出现哪种结果是无法事先确定的，这类现象称为随机现象或不确定现象。例如，掷一枚硬币，我们无法事先确定它将出现正面，还是出现反面。

教科书通过教学，使学生初步体验在现实世界中有些事件的发生是确定的，有些则是不确定的。

教科书第104页呈现了学生熟悉的“新年联欢会上抽签表演节目”的场景，引入本单元的学习。目的是从学生已有的生活经验出发，使学生体验在现实生活中存在着不确定现象，感受数学与日常生活的密切联系。

教学时，教师可以先让学生观察图意，描述图意，调动学生学习的主动性和积极性，再引导学生说一说自己在“抽签表演节目”时的实际感受。使学生在观察、描述和交流的活动过程中充分感受到，在用抽签来决定表演的节目的活动中，“表演某种节目”这样的事件的发生是不确定性的。教师还可以引导学生结合自己周围熟悉的情境，说一说在生活中还有什么事情的发生是不确定的。

需要注意的是，只要学生能够结合具体的问题情境，用“可能”等词语来描述就可以了，如“我可能要表演唱歌”。不必要求学生一定要说出“我表演唱歌这件事情的发生是不确定的”。

教科书呈现了学生摸棋子的试验，使学生在猜测、试验与交流的活动中初步体验有些事件的发生是确定的，有些事件的发生则是不确定的。

教科书中给出了两个盒子装有不同情况的棋子，是想通过两个简单试验的对比，让学生更好地体会确定事件和不确定事件。教师可以依照教科书中的图示分别在两个盒子里放进各种颜色的棋子（也可选用乒乓球等），注意这些棋子除了颜色外应完全相同，并将放棋子的过程完整地展现给学生，而且在每次摸棋子之前都应将盒中的棋子摇匀。

教科书中一共提出了三个问题，提示教学的过程、反映不同方面的要求。

①教学第一个问题“哪个盒子里肯定能摸出红棋子”。教师可以先提问“左边的盒子里肯定能摸出红棋子吗？”让学生进行猜测，再让学生实际摸摸看。通过试验，验证自己的猜测，认识到在左边的盒子里装的都是红棋子，所以一定能摸出红棋子，“在左边的盒子里摸出红棋子”这个事件的发生是确定的。教师再提问“在右边的盒子里肯定能摸出红棋子吗？”让学生进行猜测，再让学生实际摸摸看。通过试验，使学生发现在右边的盒子里有红棋子，所以可能摸出红棋子，但不一定能摸出红棋子，“在右边的盒子摸出红棋子”这个事件的发生是不确定的。

②第二个问题“哪个盒子里不可能摸出绿棋子”和第三个问题“哪个盒子里可能摸出绿棋子”可一同教学。教师可以先引导学生猜测“左边的盒子里可能摸出绿棋子吗？”“右边的盒子里可能摸出绿棋子吗？肯定能摸出绿棋子吗？”，同样再让学生讨论交流，并通过试验，验证自己的猜测，认识到因为左边的盒子里没有绿棋子，所以不可能摸出绿棋子，“在左边的盒子里不能摸出绿棋子”这个事件的发生是确定的；在右边的盒子里有绿棋子，可能摸出绿棋子，但不一定能摸出绿棋子，“在右边的盒子里摸出绿棋子”这个事件的发生是不确定的。

教学中，教师应充分地为学生提供猜测、试验与交流的机会，有条件的地方宜采取小组合作学习的方式。教师可以依照教科书中的图示，事先为每个小组准备两个盒子和两袋棋子，为了交流方便，可以给盒子标上序号1和2。在教学时，先指导学生分别将两袋棋子放入两个盒子，然后逐一提出教科书中的问题。教师还要提醒学生，在每次摸棋子前应将盒中的棋子摇匀。提出一个问题后，先让学生在小组内充分讨论、试验，然后再全班交流。使学生充分经历猜测、试验与交流的活动过程，丰富学生对确定现象和不确定现象的体验。

另外，在汇报时只要学生能够结合具体的问题情境，用“在左边的盒子里一定能摸出红棋子”“在右边的盒子里可能摸出红棋子”等描述进行表达就可以了，不必要求学生一定要说出“在左边的盒子里摸出红棋子这个事件的发生是确定的”，“在右边的盒子摸出红棋子这个事件的发生是不确定的”。

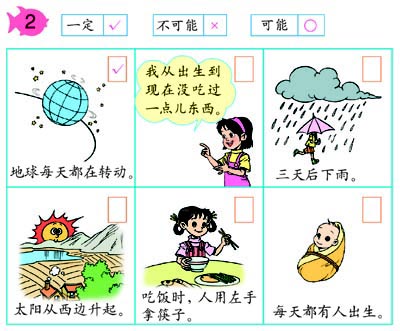
教科书呈现了六幅与现实世界的自然现象和社会现象紧密相关的画面，通过生活实例丰富学生对确定和不确定事件的认识，让学生根据已有的知识和生活经验学会判断哪些事件的发生是确定的，哪些事件的发生是不确定的。

教学时，教师可以先让学生观察图意，独立思考，根据自己已有的知识经验做出判断，再引导学生讨论。使学生在描述、思考和讨论交流的活动过程中充分感受确定和不确定现象。需要注意的是，在让学生判断事件发生的确定性和不确定性时，只要学生能够结合具体的问题情境，用“一定”“不可能”“可能”等词语来表述就可以了，如“地球一定每天都在转动”“三天后可能下雨”“太阳不可能从西边升起”等。不必要求学生一定要说出“我从出生到现在没吃过一点东西这件事的发生是确定的”“吃饭时，人用左手拿筷子这件事情的发生是不确定的”“每天都有人出生这件事情的发生是确定的”。

教师还可以引导学生结合自己周围熟悉的情境，说一说在生活中还有什么事情的发生是确定的，什么事情的发生是不确定的。另外，教师还应有意识地寻找一些带有感情色彩的事件让学生来判断其发生的确定性和不确定性，如“明天的拔河比赛我们班会赢”。让学生认识到对于某一客观事件来说，其发生的确定性和不确定性与个人的愿望无关。

2．能够列出简单试验所有可能发生的结果，知道事件发生的可能性是有大小的。

随机现象虽然对于个别试验来说无法预知其结果，但在相同条件下进行大量重复试验时，却又呈现出一种规律性，我们称它为随机现象的统计规律性。概率论正是揭示这种规律性的一个数学分支。

为了叙述的方便，把条件每实现一次，叫做进行一次试验。例如对“掷一枚硬币，出现正面”这个事件来说，做一次试验就是将硬币抛掷一次。如果一个试验在相同条件下可以重复进行，而每次试验的可能结果多于一个，在一次试验中结果无法事先确定，这种试验就叫做随机试验。把随机试验中，可能发生也可能不发生的事情，称为随机事件。

一个随机事件的发生既有随机性（对单次试验来说），又存在着统计规律性（对大量重复试验来说）。随机事件的统计规律性表现在：随机事件的频率──即此事件发生的次数与试验总次数的比值具有稳定性，即总是在某个常数附近摆动，且随着试验次数的不断增多，这种摆动幅度越来越小。我们给这个常数取一个名字，叫做这个随机事件的概率。概率可以看作频率在理论上的期望值，它从数量上反映了随机事件发生的可能性的大小。上述关于概率的定义，通常称为概率的统计定义。

由于学生的年龄和思维特点，他们一般只能在感性的层面理解概率的知识。因此，教科书通过例3、例4和例5的教学，使学生在试验活动中，认识简单试验所有可能发生的结果，初步感受随机现象的统计规律性，并知道事件发生的可能性是有大小的。

①首先，教科书呈现了一个装有两种颜色棋子的盒子，并提出一个问题“摸出一个棋子，可能是什么颜色？”目的是让学生通过摸棋子的试验，能够列出简单试验所有可能发生的结果。

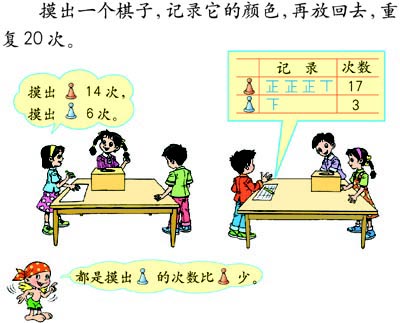
教学时，教师应注意为学生提供动手试验、合作交流的机会。使学生在观察、试验的活动中，发现从盒子里可能摸出红棋子，也可能摸出蓝棋子。进而明确，盒子里有红色和蓝色两种棋子，它们都有被摸出的可能，所以这个简单试验所有可能发生的结果，一种是摸出红棋子，一种是摸出蓝棋子。

教师还可以提问“可能摸出白棋子吗？”。通过对这个问题的讨论，帮助学生进一步明确，因为盒子里只有红棋和蓝棋两种棋子，这一试验中所有可能出现的结果也只能有两种：一种是摸出红棋子、一种是摸出蓝棋子，不可能摸出白棋子。

为了帮助学生接下来更好地理解“事件发生的可能性有大小”，教师还可以提问“是不是每一个棋子都有被摸出的可能”。引导学生发现，由于每一个棋子的形状与大小都相同，摸棋子时又不能偷看，所以摸到每个棋子的可能性是一样的。

②接着，教科书呈现了两组学生重复进行摸棋子试验并交流统计结果的场景。目的是使学生在试验、收集和分析试验数据以及讨论交流各小组统计结果的活动过程中，初步感受随机事件发生的统计规律性，并知道事件发生的可能性是有大小的。

此部分内容的学习宜采取小组合作学习的方式，教学中有以下两个方面需要注意。

第一个方面，如何组织学生进行试验。教师可以依照教科书中的图示，事先在各小组的盒子里放进两种颜色的棋子。在做试验前，教师首先要使学生明确试验的过程，“摸出一个棋子，记录下它的颜色，再放回去，重复20次”。然后还要使学生明确组内成员的分工，应有人负责摸出棋子，有人负责记录下它的颜色，并应提醒学生在试验前要选择好统计试验数据的方法。而且还要向学生说明在试验的过程中，应注意保证试验的随机性，如：每次摸棋子前应将盒中的棋子摇匀；摸棋子时不要偷看等。在各小组进行试验的过程中，教师应关注每一个小组，及时给予指导，保证试验的随机性。

首先，教师可引导学生交流对随机现象的不确定性的体验。如，让学生说一说每次摸到棋子的情况。在每次摸的时候，每个棋子都有被摸出的可能；每次摸到的棋子的颜色是不确定的，可能摸出红棋子，也可能摸出蓝棋子。

然后，再通过讨论使学生初步感受随机事件发生的统计规律性。教师应引导学生不只关注本小组的统计结果，还要分析所有小组的统计结果有什么共性。如提问“每一个小组的统计结果都一样吗？”“所有小组的统计结果有什么相同的地方？”，引导学生发现，虽然每次摸到棋子的结果不确定，但当大量重复试验时，试验结果就呈现了一种规律性，都是摸出蓝棋子的次数比红棋子少。教师还可以将全班各小组的试验结果进行汇总，以加深学生对随机试验统计结果规律性的直观感受。

最后，教师再引导学生发现事件发生的可能性是有大小的。如提问“摸出哪种棋子的次数多”“盒子中红棋与蓝棋的数量相等吗”，使学生认识到，在这个摸棋子的随机试验中，每一个棋子被摸到的可能性是相等的，红棋子与蓝棋子的数量不等，那么摸出红棋子的可能性与蓝棋子的可能性是不一样的。红棋子的数量多，摸出红棋子的可能性就大。

③最后，教科书提出了一个问题“再摸一次，摸出哪种颜色的棋子可能性大”，让学生根据试验的统计结果对下一次试验的结果作出推测。

在学生进行推测后，教师可以再让学生实际摸摸看。学生很可能摸出红棋子，但也有可能摸出蓝棋子。通过试验使学生认识到，虽然我们知道了摸出红棋子的可能性大，但在单次试验中我们并不能确定会摸出红棋子。进一步感受不确定现象的特点，体会概率虽然能够帮助我们了解这些不确定现象的规律，但概率并不提供确定无误的结论，这是由不确定现象的本质造成的。

教科书中设计了一个简单的转盘游戏，使学生在生活经验和试验的基础上，体会指针停在哪种颜色的区域内的可能性大。

教师可以事先仿照教科书上的转盘，为每个小组做两个指针可以自由转动的转盘。在教学中，教师可先让学生说一说这个简单游戏中可能发生的结果有哪些，并让每一个学生预先猜测指针会停在哪种颜色的区域内，然后动手旋转指针，提醒学生记录每次试验的结果。让学生在亲自旋转指针的过程中体会，当指针没有停下来以前，指针停在哪个区域内是不确定的，通过多次旋转后学生逐渐体会指针停在两个区域内的次数不一样。以左题为例，停在黄色区域内的次数比停在红色区域内的次数要多，即指针停在黄色区域的可能性比停在红色区域内的可能性大。在学生动手操作的基础上，教师可以引导学生开展讨论，交流自己的感受。使学生认识到在左题中，黄色区域的面积大，红色区域的面积小，因此指针停在黄色区域的可能性大。在右题中，蓝色区域的面积大，黄色区域的面积小，因此指针停在黄色区域的可能性小。

教科书中在这里设计了另一个摸棋子的试验，使学生进一步体会不确定现象的特点及事件发生的可能性的大小。

①首先，让学生列出简单试验所有可能发生的结果。与例3相比，增加了一种颜色的棋子，这个简单试验可能发生的结果增加到了三个：摸出红棋子、摸出蓝棋子、摸出绿棋子。

需要注意的是，通过例3的教学，学生已经借助试验能够列出简单试验所有可能发生的结果。这里，教师应引导学生根据盒子里棋子的颜色种类列出这个简单试验所有可能发生的结果。如果学生有困难，教师再通过试验帮助学生理解。

②接下来，让学生判断摸出各种颜色棋子的可能性大小。将三种可能出现的结果的可能性进行比较，要让学生能够判断出摸出哪种颜色的可能性最大，摸出哪种颜色的可能性最小。

通过例3的教学，学生已经在试验、收集和分析试验数据以及讨论交流的活动过程中，获知了判断事件发生的可能性大小的方法。教学时，教师可以先让学生猜测摸出各种颜色棋子的可能性大小，再让学生小组合作，设计一个简单的实验来验证自己的猜测。由于学生已经在前一部分内容的学习中获得了一些进行实验的经验，教师只需引导学生说一说设计这个实验时需要注意什么，如“实验的次数要足够多”“每次摸棋子前要将盒子里的棋子摇匀”等，然后放手让学生去实验。在各小组进行实验的过程中，教师应关注每一个小组，有针对性地进行指导。最后，各小组汇报交流，使学生进一步体会不确定现象的特点及事件发生的可能性的大小。

教科书通过让学生根据摸棋子试验的统计结果来推测袋中何种颜色的球多，并实际验证，进一步体会随机事件发生的统计规律性。

教师可以为每个小组准备一袋棋子，注意两种颜色的棋子的数量相差要大一些。然后让学生仿照例3进行试验，再根据试验的统计结果进行推测“哪种颜色的棋子多”，最后再打开袋子看一看，验证自己的猜测，获得成功的体验。在学生动手操作的基础上，教师可以让各小组进行汇报，引导学生开展讨论，交流自己的感受。重点让学生说一说统计的结果是什么，自己的猜测是什么，为什么这样猜。

（4）第107页的“做一做”。与教科书第106页的“做一做”相似，设计了一个简单的转盘游戏，使学生在试验的基础上，判断指针停在哪种颜色的可能性最大，停在哪种颜色的可能性最小。教师可以仿照教科书第106页的“做一做”进行教学。由于将颜色增加到了三种，学生可能不易直观看出哪种颜色区域的面积大，教师可引导学生用已有的分数知识说一说各种颜色区域占总面积的几分之几，并比较它们的大小。

第1题，通过实际例子，让学生体会客观世界不但存在着确定事件，也存在着不确定事件。

第2题，让学生涂色使结果符合要求，帮助学生更加深刻地理解确定和不确定现象。第（1）题，只能有一种涂法。第（2）（3）题是两道开放题，学生会有很多种涂法。可以先让学生独立思考、设计涂色方案，并动手实践，然后在全班展示。在学生展示自己的涂色结果时，重点要让学生说一说自己的想法。

第3题，让学生根据自己已有的知识和生活经验，用“一定”“不可能”“可能”进行表述，使学生进一步感受生活中有些事情的发生是确定的，有些则是不确定的。可采用灵活的练习方式，如可以让学生用“一定”“不可能”“可能”描述一件事情，也可以让学生说一个事件，其他同学用“一定”“不可能”“可能”进行判断；可以在小组内进行，也可以全班一起完成。

第4题，让学生涂色使结果符合要求，帮助学生更加深刻地理解事件发生的可能性的大小。这是一道开放题，学生会有多种涂法，只要圆盘中两种颜色区域的面积大小有差别就可以了。可以先让学生独立完成，再在全班展示，并让学生说一说自己的想法。

第5题，让学生用简单的实验来验证自己的猜测，进一步理解事件发生的可能性的大小。由于学生已经有了一些进行实验的经验，可以先让学生独立完成，再在小组内交流。

第6题，是一个掷硬币的游戏。我们设计这道题目，是想通过掷硬币试验，使学生初步感受事件发生的等可能性。教师可先让学生说一说掷出后可能出现的结果有哪些，再让学生猜测实验后的结果（即正面、反面出现的次数）会有什么特点。让全班一起掷一次，是为了使试验次数足够多，以减少误差。由于实验结果与理论概率存在的差异，也可能得不到预期的结果，可以再让学生掷几次，增加试验的总次数，尽量使实验结果接近理论概率。然后，再引导学生讨论正面、反面出现的次数的特点。让学生根据试验的结果初步感受到硬币是均匀的，两种结果出现的可能性是相等的就可以了，不必要求学生用概率术语进行表述。

第7题，通过两个简单试验的对比，让学生更好地体会事件发生可能性的大小。教师应引导学生根据两个盒子里绿色球的数量判断哪个盒子里摸出绿球的可能性大，要注意提醒学生这两个盒子里球的个数是相等的。如果学生有困难，可以通过试验帮助学生理解。还可以改变两个盒子里球的数量，如在第1个盒子里放10个球，第2个盒子里放30个球，两个盒子里都有5个绿球，让学生判断哪个盒子里摸出绿球的可能性大。需要注意的是，只要学生能够借助直观感受和试验，用“很可能”“不太可能”等词语来描述可能性的大小就可以了，并不要求学生求出可能性的具体大小。

第8题，是一个掷骰子的游戏，使学生进一步感受事件发生的等可能性。教学建议与第6题相同。

第9题，通过有趣的抽签游戏，让学生体会不确定事件发生的可能性的大小。还可以让学生用“最不可能”和“很有可能”说一说其他两个事件发生的可能性。

第10题，是一个猜一猜的游戏，让学生进一步感受不确定现象的特点和事件发生的可能性的大小。教师可先让学生猜测硬币可能在哪个盒子里，让学生体会这四个盒子都有可能。在统计猜测结果的时候，注意要求每个学生只能选择一次，不能重复选。然后，再让学生讨论统计结果有什么特点，引导学生发现，硬币只能在四个盒子中的一个，有三个盒子中没有，所以猜错的人数多，猜错的可能性大。教师还可以重新放置硬币再让学生猜几次，并让学生说一说自己几次猜测的情况，引导学生体会，虽然我们知道了猜错的可能性大，但在单次试验中我们也有可能猜对，进一步感受不确定现象的特点。

第11题，让学生涂色使结果符合要求，帮助学生更加深刻地理解事件发生的可能性的大小。这是一道开放题，学生会有多种涂法，只要涂色后正方体的红色面比蓝色面的数量多就可以了。教师应先教学生用硬纸板做一个立方体，可以让学生独立设计涂色方案，再用实验证明自己的设计符合要求，并在小组内进行展示，重点让学生说一说自己的想法和实验的情况。也可以让学生小组合作完成，并在全班交流。

第12题，让学生设计一个方案使结果符合要求，帮助学生更加深刻地理解事件发生的可能性的大小。这是一道开放题，学生会有多种方案，只要写有数字“1”的卡片数量最多，写有数字“5”的卡片数量最少就可以了。教学建议与第11题相同。