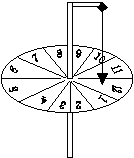
尽管数学起源于生产实践，但历经数千年的演变发展，现行课本中的数学知识大多已完全脱离了最初蕴育数学发展的基壤，使得绝大多数学生认为数学是抽象的、没有生机的学问。难道数学真是远离生活的科学吗？不。数学的发展之所以几乎与人类的文明同步，就是因为它充满了生机与活力。解放前，在城镇的大路旁边，有时见到各种碰运气、赌输赢的小摊。其中的一种，叫做转糖摊。笔者在初一代数式教学中，模拟了“转糖摊”小游戏，上了一堂生动活泼的数学活动课，完成了一次对数学知识的探索、发现过程，使学生真正体验到“数学为之用”的道理。

【课前准备】一块圆形纸板，一根粗铁丝，一根线绳，绳头系一重物。

【道具制作】在圆形纸板上画12个扇形格子，顺次序编上号，做成一个圆盘；粗铁丝穿过圆盘中心，做成一个可以转动的轴；轴的上端向外垂直伸出一根悬臂（可将粗铁丝折成90°做成），悬臂端吊一根绳子，绳头上有一重物做为指针。

学生课前就知道要做游戏，一直不知道做什么游戏，心存悬念，充满热情地帮助教师制作道具。

【虚拟游戏规则】假设在圆盘的1号、3号、5号、7号、9号、11号格子里放上价值10元的物品，在2号、4号、6号、8号、10号、12号格子里均放上价值5角钱的物品。谁交上1元钱（假设），就可转一下圆盘，等停转后，指针指到哪一格，便根据那格的数，从下一格起，按格往下数这个数，数到哪一格，放在格里的物品就归谁。

教师边演示边说明游戏规则，学生热情高涨，跃跃欲试，心想：盘子上，单数和双数格子各占一半。数到双数得“5角钱”，虽然亏了；数到单数得“10元钱”，可就赚了。“1元钱”不多，可以碰碰运气。于是争相排队等候，看看谁能得到“10元钱”。

一个学生摇了个3，其它同学都积极参与，帮他算出是6，“1元钱”换了“5角钱”，赔了。

第二个学生马上又摇了个6，结果师生共同算出12，又赔了。这时在众多挤着向前一试的同学后面，就有同学有疑问了，开始动脑了。又几个同学试过了，还是没有得到“10元钱”。只见有几个同学脸上露出了笑容，齐声喊到“没有10元钱，没有10元钱，老师骗人，老师骗人”，而其它同学有的似乎也明白了，有的还想试试，有的却愣住了。

师：为什么说老师骗人呢？

生1：按照这样的数法，是怎样也得不到“10元钱”。

师：为什么呢？

生2：单数的格子里放着价值10元钱的物品，双数的格子里放着价值5角钱的物品。按照这样的数法，是怎样也数不到单数格子上去的。

师（及时点拔）：单数、双数也就是……

生3：单数也就是奇数，双数也就是偶数。

师：为什么数不到奇数格子上去呢？

生4：我一个一个地试过了，不管我摇得几，最后都数到偶数格子了。

师：为什么会出现这种情况呢？

生：……（说不清）

还有部分同学在皱着眉头不知所向。于是教师边板演边说：假如我摇了个奇数3，3+3＝6,6是个偶数；假如我摇了个偶数4，4+4＝8,8也是个偶数。

生（抢答）：我明白了，道理很简单，因为：

奇数+奇数＝偶数；

偶数+偶数＝偶数。

这就是说，不管指针指在奇数还是偶数，最后数到的总是偶数格，赚的可能性是零。

全体学生都露出了笑容，同学们明白了。师把结论写在黑板上。

师：解放前，在城镇的大路旁边，经常见到各种碰运气、赌输赢的小摊。我模拟了其中的一种，叫做转糖摊，却被同学们识别了我的“诡计”。说明我们同学学了数学，就会用数学。

教师及时给学生以成功的喜悦，使学生的热情达到高潮。进一步引导学生回顾小学所学习过的奇数偶数的概念，并运用刚刚学到的代数式的知识，来证明上述结论确实成立；同时又提出奇数+偶数的疑问，并经过证明得出奇数+偶数＝奇数

的结论。

师：通过这节活动课，同学们学到哪些知识？还有哪些想法？

生1：我知道了奇数+奇数＝偶数；偶数+偶数＝偶数；奇数+偶数＝奇数，还复习了奇数偶数的概念。

生2：小学的时候，都是老师教给我们一些知识，现在我明白了，有时我们自己也可以发现一些道理。

生3：不管什么道理，都得经过证明，才能说它是正确的还是不正确的。

生4：老师，我还发现，我们学了数学，要会用数学才行，否则我们不就“上当”了吗？

生5：我还可以利用奇数+偶数＝奇数来改造一下这个游戏。我把价值10元钱的物品放在偶数格子里，把价值5角钱的物品放在奇数格子里。规定指针指在哪一格，便根据那格的数，从这一格起，按格往下数这个数。

同学们畅所欲言，纷纷发表自己的见解，直到下课同学们还在讨论。

纸上得来终觉浅，绝知此事须躬行。在日常教学中我们要从多方位、多角度着手培养学生用数学的意识，不能单纯看重解应用题和常规建模教学，而将“数学之为用”论为新的“应试”训练，达不到提高学生综合素质的目的，难以真正实现培养学生“用数学于现实世界”的意识和能力。我们应通过创造性的数学活动，让数学应用意识化为信念，伴随学生的学习与生活，成为终生享用的财富。