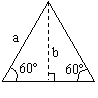|
图形求积的综合练习 |
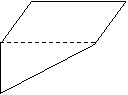
教学目的:1、进一步学会观察图形中线段位置、数量之间的关系;2、掌握几种常用的求积方法3、能灵活运用平行四边形、三角形和梯形等基本图形有关公式解决求一些组合图形的面积。 教学内容:教材第131页第28-31题 教学过程:复习已经学习过的五种图形的面积计算公式; [提问:同学们到目前为止我们已学过了哪些图形?(放幻灯片1)
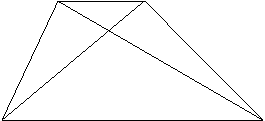
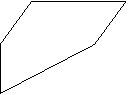
通过拉动梯形的一条底来揭示梯形、三角形和长方形面积计算之间的关系。
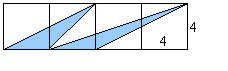
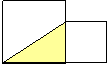
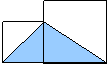
[老师:有了这些图形的面积计算公式,我们就可以根据图中的已知条件来解决有关的问题(放幻灯片2)]
你还能否知道图中哪些三角形的面积与阴影三角形面积相等?(让学生用几何画板画出与之相等的三角形)
以上问题还可以少出现2-3个,让学生能否在图中自己画出一些三角形,并使其面积等于图(1)。 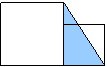 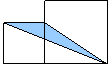
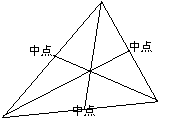
让学生用几何画板画出相等的三角形) 5、利用有关公式求组合图形的面积:
解决本题的思路:
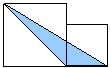
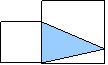
(3)右图中梯形下底6厘米,高3厘米,AB=2厘米, 求阴影部分面积之和。 6、小结:(1)各种图形的面积计算公式是相互联系的;(2)求组合图形的面积的关键是如何把它们转化成若干个基本图形,并运用适当的方法(分割法、去除法、等积变形法)进行解决。 7、作业(略)
|