|
梯形面积的计算 |
福田区水围小学 冯卫忠 教学内容:人教版第九册第74-75页“做一做”。练习十八第1、2、3题。 教学目的:1、理解并掌握梯形面积公式的推导过程,正确进行梯形面积的计算。 2、培养学生分析、综合、抽象、概括的能力,发展学生的空间观念。 教学重点:使学生理解和掌握梯形的面积公式,能正确应用面积公式计算梯形的面积。 教学难点:使学生理解梯形面积公式的来源,理解为什么要除以2。 教学用具:多媒体课件一套、投影仪。学生分小组分别准备4个形状大小完全相同的梯形。 教学过程:
的面积你会计算吗?这节课我们就来学习梯形面积的计算。 板书:梯形面积的计算
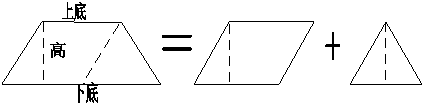
学生拿出准备好的梯形分小组讨论,拼一拼,摆一摆,看能想出几种方法。 学生操作,把拼好的小组代表请到展示台演示过程并简略说理由: 方法一:学生用两个大小一样的梯形拼成一个平行四边形,
梯形面积=平行四边形面积÷2
方法二:把梯形沿对角线剪成两个三角形, 梯形面积=三角形1面积+三角形2面积 法三:沿梯形上底的一角顶点到下底任一点作对边的平行线,把梯形分成一个平行四边形与三角形。
方法四:``````
同学们都很聪明能想到那么多种方法求梯形面积。那么我们能不能总结出梯形面积的计算公式呢? 请同学观察方法一,分小组思考讨论:
5) 怎样求出梯形面积? 师根据学生回答归纳出:梯形的面积=(上底+下底)×高÷2 (板书) 师问:为什么要除以2? 梯形的面积计算公式还可以用字母表示。请生看课本75页,理解并记住梯形面积的计算公式。 请同学们看方法二: 你能根据这种方法也算出刚才梯形的面积吗? 学生分小组计算出计算式:3×4÷2+5×4÷2 师再引导学生根据和除以一个数规律和乘法分配律想出3×4÷2+5×4÷2=(3+5)×4÷2(也就是上下底之和乘以高除以2) 师:方法二也是一种很好的方法。方法三呢?课后留给同学们自己看能否也概括出方法一、方法二中的梯形面积公式。
学生理解“横截面”:(教师利用 电脑演示水渠的横截面形状)、学生试做,集体订正、 四、 学生质疑本课相关问题,调动学生互问互答积极性,教师引导。 五、技能应用: 1. 电脑出示各种位置的梯形,学生口答各梯形的上下底和高,让学生说说怎样确定梯形的上下底和高。 2. 做课本75页“做一做”,独立完成,集体订正。 3. 电脑出示课本76页圆木或钢管堆放图,学生思考:怎样算出总根数? 分小组议一议,并说明理由。 六、 课后作业:课本76页1、2、3题 板书设计
梯形面积的计算 例1:一条新挖的渠道,横截面是梯形(如图),渠口宽2。8米,渠底宽1。4米,渠深1。2米 。它的横截面积是多少平方米? (2.8+1。4)×1。2÷2 =4。2 ×1。2÷2 =2。52(平方米) 答:它的横截面积是2。52平方米。 平行四边形的面积= 底 × 高 2个梯形面积 =(上底+下第)× 高 梯形面积 = (上底+下第)×高 ÷2 s = (a+b) · h ÷2 |

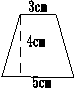 平行四边形、三角形的面积我们已会计算了,那么这个图形(多媒体出示梯形)
平行四边形、三角形的面积我们已会计算了,那么这个图形(多媒体出示梯形)