一、背景介绍
图形的变换主要有两种方式:平移和旋转。本教材是在平移转换的基础上学习旋转变换,进一步引导学生用运动的眼光看待生活中的图形,并通过揭示图形的变化规律和内在联系,促进学生观察、分析、归纳、探究能力的提高,既能培养学生积极的情感和态度,又能增强他们学数学、用数学的信心。
二、教学设计
〔教学内容分析〕
本节通过生动的实例,让学生感受生活中的旋转现象,直观地认识旋转变换,并在此基础上,分析旋转现象的规律,得到旋转变换的性质,然后利用性质进行简单的旋转作图,进一步深化对图形变换的理解和认识,体会旋转变换的应用价值和丰富内涵。
〔教学目标〕
1、经历对生活中旋转现象的观察、分析、欣赏,认识图形的旋转变换。
2、探索图形旋转变换的要素和性质,能按要求做出简单图形经过旋转变换后的像。
3、培养学生良好的情感态度和审美情趣,提高观察、分析、抽象、表述等各方面的能力。
〔教学重点〕
图形旋转变换的性质
〔教学难点〕
旋转变换的作图及旋转过程的叙述
〔教学准备〕
放影片 三角板
〔教学过程〕
|
教 学 过 程 |
设 计 意 图 |
一、创设情景,引出新课
1、放影:杭州未来世界的转盘;运动会上自行车比赛中的车轮;转动的风扇;钟表的指针……
(1)你看到了哪些现象?
(2)在各自的转动过程中,哪些改变了?哪些保持不变
2、投影:节前图
(1) 风车的叶片由A至B的运动与静止的自行车踏脚板的轴由C至D的运动有什么共同的特点?
(2)你是从哪些方面考虑的?
引导学生从运动物体各部分旋转的方向和角度考虑。
二、交流对话,探究新知
1、旋转变换的概念
试一试:你能用语言描述一下图形的旋转变化吗?
在描述的基础上,老师补充、归纳出旋转的概念,并强调旋转变换的三要素:中心、方向、角度。
想一想:你能举出生活中旋转变换的例子吗?
做一做:(1)回答教科书53页的两个问题 学生的回答可能不太准确,教师明确:描述一个旋转变换,必须抓住旋转中心、旋转方向(顺时针或逆时针)、旋转角度三个关键。
(2)如图所示的图案,它可以看作是哪
一个图形,通过怎样的旋转而得到的?
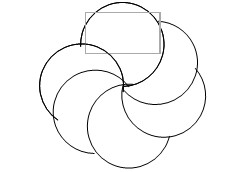
学生的回答可能是把6条中的一条作为基本图案,也可能把相邻两条曲线、相对两条曲线、相邻三条曲线、“风扇”形曲线作为基本图案,只要描述合理,教师都要予以认可。
2、旋转变换的性质
画一画:四位学生分两组,板演:沿三角板的边
画△ABC,再将三角板绕顶点A旋转任
一角度,沿各边画出△ADE。
C  D D
B   E E
A
议一议:在这个旋转变换中
(1)旋转中心是什么?
(2)经过旋转,点B、C分别移到什么位置?
(3)AC与AE的长有何关系?AB与AD呢?
(4)∠CAE和∠BAD有什么大小关系?
试一试:你能不能根据上题的结论,总结一下旋转变换的性质呢?
在学生回答的基础上,老师补充、归纳出性质。
三、应用新知,体验成功
1、例题:教科书54页
采用教师点拨,学生独立操作的方式处理。也可采用分组讨论、合作交流、小组展示成果的方式处理。
教师规范作法的文字叙述。
2、反思:求作一个图形的旋转变换,关键是什么? 在学生回答的基础上,教师明确:求作一个旋转变换,可以先将图形上的某些点作旋转变换,然后根据旋转变换不改变图形的形状、大小、以及点线之间的位置关系等性质,作出原图形的像
四、归纳小结,形成结构
通过本节课的学习,你有哪些收获?
1、旋转变换的要素及性质
2、如何按要求作出一个图形旋转变换的像。
五、布置作业 |
创设情景,激发学生的兴趣,初步感受旋转。
通过观察、分析、归纳旋转变换的特征。
学生用语言描述,既培养了他们的表达能力,又建立了自信,从而认识旋转。
通过思考、回答和交流,发展他们的思维能力。
加深对旋转变换的理解,激发学生的兴趣,培养他们的探究、创新能力。
使学生参与数学活动,激发兴趣,培养合作意识。
通过对具体问题的交流探索,体验知识的形成过程。
鼓励学生自主交流操作,培养他们分析问题、解决问题的能力。
总结学习过程中的体验和收获,增加学习数学的信心。 |
设计思路:
1、 本节课是按“创设情景—交流合作—探究新知—形成规律—应用新知—反思提高”的模式展示知识的形成过程,符合学生的认知规律,
2、 通过生活中的实例,创设问题的情景,激发学生的学习兴趣;通过师生互动,讨论、发现、自主探索、交流合作丰富学生的数学活动经验和体验,既可以培养他们积极的情感、态度,又可以促进观察、分析、归纳、概括、探究等能力的提高,充分体现了“新课标”的教学理念。
3、 教学方式的开放性,注重优化学生的思维品质,以引导学生形成正确的数学观,增强他们学数学、用数学的信心。
教学后记:
学生能理解“旋转变换”的性质,但不能很好地运用它。特别是叙述一个旋转变换时最容易忽略它的三要素。
|




 E
E