|
《三位数乘两位数的口算乘法》内容说明和教学建议 |
1.小节说明 本小节的教学是口算乘法。涉及的内容有:两位数乘一位数(积在100以内)和几百几十的数乘一位数。这些内容是义务教育阶段有关整数口算乘法的教学目标,它是作为一个公民应该具备的口算乘法技能的基本要求。 学生学习本单元口算的知识基础是:会口算整十、整百的数乘一位数(或整十数),能笔算两位数乘一位数、两位数。根据学生已有的这个知识基础,教材只安排了一个例题,其中第(1)小题(15×3)教学两位数乘一位数(积在100以内),第(2)小题(150×3)教学几百几十的数乘一位数。两个小题从问题情境到计算数值和计算方法都密切相关,期望学生通过这两题的学习能自主掌握整数乘法的一般口算方法。 2.例1 编写意图:
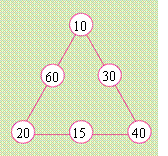
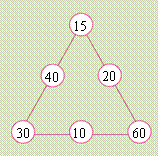
(2)以物体的运动为背景,选择两个来自生活实际又具有特殊数值的两道算式16×3、160×3作为引导学生学习口算的范例,使学生通过对比,自主得出一位数和两位数(或几百几十的数)相乘的简便算法。 (3)鼓励学生在自主思考的基础上,与同伴交流。如第(1)题中两同学交流的画面。通过交流,引导学生思考不同算法中的特点,从而选择能理解又优化的一种算法。 教学建议: (1)课前可要求学生通过不同的渠道查找自己知道的一些交通工具的运行速度。除教科书第45页呈现的6种交通工具的时速外,学生一定还能找出更多的交通工具的时速,如摩托车、大型货车、客车、江轮、海轮……等等,这些由学生查找出来的交通工具的时速,都可作为本单元学习的资源。 (2)教学例1第(1)题时,应提示学生用自己的知识经验独立口算,教师巡视时,注意统计不同口算方法的种类,汇报交流时,让不同算法的学生在班上交流,而后引导学生对比不同算法的特点,使每个学生都能从自己或他人的算法中确立一种合适的算法。 (3)以“16×3”为基本口算,在此基础上学习它的相关变式:“160×3”或“16×30”。教学时,先引导学生纵向对比第(1)、(2)小题,让学生从16和160的关系中,总结出几百几十与一位数相乘的口算方法。然后将第1题增加1个条件“30小时行多少千米?”,得出两位数乘整十数的算式“16×30”,让学生在与“16×3”的对比中归纳出简便算法。 (4)本小节可用2课时进行教学。 3.关于练习六中一些习题的教学说明和教学建议 第1题,是让学生形成基本口算能力的练习。练习时,必须采用人人参与的口算形式。如让每位学生独立口算,将得数写在该题(树叶)的旁边,然后让部分学生说一说计算的过程,及时反馈学生口算情况。 第2.3题是应用口算乘法解决实际问题。第2题的练习功能有二:①巩固本小节所学口算知识;②了解两种常见花卉的品种。练习时,可向学生展示两种花卉的部分品种,引发学生的生活美感。第3题是开放题,解法有:①18×3=54,54<60,可买3份左图所示食品;②18×2+21=57,57<60,可买2份左图所示食品和1份右图所示食品;③18×1+21×2=60,可买1份左图所示食品和2份右图所示食品。练习时,不要求每位学生都做出3种答案,但在反馈学生解答结果的过程中,应引导学生学会有序思考的方法。另外,还可充分利用本题信息资源,扩大解题视野。如可提问学生:买3种右图所示食品,钱够吗?如不够,还差多少? 第4~7题可作为第2课时的巩固练习用。第4题是提高学生口算熟练程度的练习。期望在充分理解算理、正确应用算法的基础上,提高运算的正确性和速度。练习时,仍要采用人人参与、独立口算的形式。尽可能使每一位学生算得正确,并有一定的速度。 第5题蕴含了函数思想。通过两组练习,使学生感悟“一个因数扩大若干倍,另一个因数不变,积也扩大相同的倍数。”学生练习后,应让学生自主说出(或小组讨论得出)积随因数变化的情况,为后面学习“积的变化规律”作些孕伏。 第6题的练习应让学生体会在解决具体问题的过程中,如何选择合适的估算方法。例如,因为25×4=100,24<25,所以带100元够用。同时在估算过程中,学会有理有据的进行表达,培养推理能力。 第7题的呈现方式是市场促销中常用的方式,如“买3棵送1棵”。练习时,应让学生咀嚼题意,在理解题意的基础上,学生的解答思路才有可能跳出常规思维的套路,才有可能创新。如学生可能这样作答:16÷4=4(元)。理由是:“买3棵送1棵”相当于买4棵少收16元钱,则平均每棵少收4元钱。这样简明快捷的解答就是基于对题中信息深刻的理解。对小学生来说,有别于常规思路的解答就可以说是创新。 第8题是引导学生探索数值间规律的练习。其中“220+230+240+25=( )×( )”一题,答案不唯一。可以是“235×4”,也可以是“470×2”。 最后的思考题是供学有余力的学生学习的,具有一定难度。应引导学生从6个数据的关系中找出规律,然后再填空。此题属于数阵图问题,体现了数形结合的美,可以培养学生全面地思考问题的习惯和推理能力。如果从一般化的建立模型的角度思考,可以先假设这6个圈里的数分别为a、b、c、d、e、f,如图所 根据题意,可知afb=bdc=aec即af=dc,fb=ec,bd=ae。 由此可得a:b=d:e,b:c=e:f,即a:b:c=d:e:f。 也就是说,只要满足这样的条件:三角形中三个顶点上的三个数的连比等于三条边中间三个数的连比(如上所示),再按照右图把6个数填入圈中便可。 下面再根据上面的思路把6个数分成2组,能够组成两个相等的连比形式。从6个数中不难发现10.20.40,15.30.60这2组数分别存在着相同的倍数关系,可得10:20:40=15:30:60。 答案如图所示。
由于学生还没有学习比和比例的知识,教师可以把这种思想方法用乘法、除法、倍数关系等学生容易理解的形式介绍给学生。 |

 (1)从本单元主题图中选择出自行车和特别快车的运行速度为素材学习口算。使学生在熟悉的生活情境中,激发探究的欲望,同时通过了解不同交通工具的运行速度,理解用复合名数表示的数学术语“速度”的含义,为后面理解关系式“速度×时间=路程”作好铺垫。
(1)从本单元主题图中选择出自行车和特别快车的运行速度为素材学习口算。使学生在熟悉的生活情境中,激发探究的欲望,同时通过了解不同交通工具的运行速度,理解用复合名数表示的数学术语“速度”的含义,为后面理解关系式“速度×时间=路程”作好铺垫。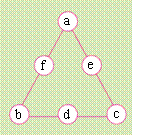 示。
示。