1．角的度量。

教材分两个层次编排。第一个层次，是介绍量角器和角的度量方法。首先，借助两个学生比较角的大小的情境图，引出“量角的大小，要用量角器”，指出角的计量单位是度，再拿半圆分成180等份说明1°角有多大，并配以1°角的直观图示，使学生形成1°角的正确表象。接着让学生讨论用量角器量角的方法。第二个层次，让学生通过对两组角的度量，进一步明确：角的大小要看两边叉开的大小，与所画的边的长短无关。

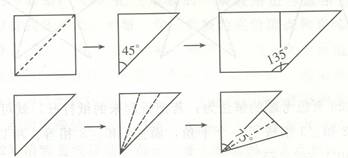
“做一做”的三道题目，在进一步巩固量角方法的同时，注意让学生积累一些常见的角的大小的表象和估计意识的培养。例如，第1题，让学生观察量角器，看一看30°、45°、60°、90°、120°的角分别有多大；第3题，要求学生先估计再量一量三角尺上各个角的度数。

教学时要充分估计学生学习的起点，给予学生自主学习的空间。首先，可以让每个学生画一个角，同桌间比较角的大小。引导学生探讨并发现：当两个角不能直接比较大小的情况下，可以用量角器测量出各自的度数，再进行比较。接着，可以要求学生先自己尝试量一量所画角的度数。反馈时，再引导学生观察量角器的构造，看一看上面的刻度和数据，并归纳量角的方法。应强调：用量角器量角的时候，把量角器放在角的上面，使量角器的中心和角的顶点重合，零度刻度线和角的一条边重合，角的另一条边所对的量角器上的刻度，就是这个角的度数。关于量角的具体步骤，教材给学生留出了思考和探究的空间，需要教师加以补充说明。然后要求学生量出教材上∠1和∠2的度数，并比较测量的方法的异同，从而理解量角器上两排刻度的用处。在完成“做一做”三道题目的基础上，再组织学习例1。让学生通过两组角的测量再次感悟角的大小要看两边叉开的大小，与所画的边的长短无关。

2．关于练习四中一些习题的说明与教学建议。

练习中加强操作，通过第3、5、6、7等题，让学生折纸和用三角板拼摆出、量出、画出一些特殊度数的角，使学生加深对这些角的大小的印象，培养初步的空间观念。

第3题，要求说出每个钟面上的时间，量出时针和分针所成的角的度数。一方面用来巩固量角的方法，另一方面联系生活实际，带着复习以前学过的知识。

第5题，要求用一张正方形纸对折两次，打开后再沿一条对角线对折，再打开，然后分别找出45°、90°、135°的角，如果学生有困难，可适当启发。折成直角后，再折一折，就是45°，打开一个直角，就组成135°。把一个45°角平均折成3份，取两份，再和45°角合在一起就拼成75°角了。

第6题，要求用一副三角尺拼出75°、105°、120°、135°、150°、180°的角。如果学生有困难，可以提示他们先想一下两个三角板每个角各是多少度，然后启发学生想，利用三角板上的角怎样组合才能拼出题目中要求的各个角度。

第7题，要求学生量出各角的度数，说一说发现了什么。由于这四个角之间的特殊关系，在巩固量角方法的同时，也为平角和周角的学习作些准备。