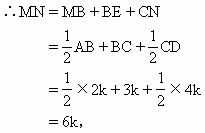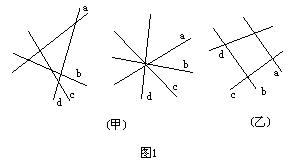
一、数学抽象与数学语言

点、线、面、体都是几何的基本元素，它们都是从现实世界客观存在的事物中抽象出来的概念，但是这种抽象又不是具体事物的简单映象，而是把事物共同的本质的特征或联系抽取出来，而舍弃个别的非本质的特征和联系．如点是针尖、用笔尖在纸上画出的小点等实例的抽象，但几何中的点只表示位置，没有大小；直线是拉紧的细线、直尺的边缘等实物的抽象，但几何中的直线是向两方无限延伸着的。从实物中抽象出来的数学概念在我们面前呈现出的是图形，表示这些图形的符号，叙述它们性质的文字。数学的抽象相应产生了数学的语言。

几何中的数学语言按形式不同有文字语言，符号语言和图形语言，在学习平面几何的起始阶段，理解这些语言，学会这几种语言的应用和互相转换是十分重要的。

例如：平面上有A、B两点，画出直线AB，射线AB和线段AB的画法语言及相应的图形就是不同的：画直线AB要用“过点A，B作直线”，而不能用“连结AB”。后者是画线段AB的数学语言。也不能把“连结”写成“联结”或“联接”“连接”。语言的规范化对于培养流畅的、正确的数学思维是十分必要的。

爱因斯坦说过：“科学必须创造自己的语言和自己的概念供它本身使用，科学概念最初总是日常生活中所用的普通概念，但它们经过发展就完全不同，它们已经变换过了，并失去了普通语言中所带有的含糊性质，从而获得严格的定义，这样它们就能应用于科学的思维。”

几何中的“有且只有”，“确定”，“直线a，e，c，d两两相交”等等在数学中就有其确定的含义，“4条直线a，b，c，d两两相交”是指每两条都相交，它所对应的图形为图1（甲）而不是（乙）。

在几何中还出现了大量的符号语言，它们也有其特定的意义。本章中，简单的，基本的图形的文字语言、符号语言和图形语言之间的熟练转换将为更复杂的图形的学习打下基础。

二、数与形的结合

以图形的认识为主，这是几何研究的主要特点，同时联系到数量，使两者一致起来，达到形和数的结合。

数和形是数学的两块基石，它们常常结合在一起，在内容上互相联系，在方法上互相渗透，在一定的条件下可以互相转化。数形结合作为一种重要的数学思维方法，就是在上述背景下形成的。

在解题过程中，必须注意把数和形结合起来考察，把形的问题转化为数的问题，或者把数的问题转化为形的问题。利用数研究形，关键在于创设条件，使几何图形数量化。

例1 在直线l上，按一定的方向顺次取点A，B，C，D，且使AB∶BC∶CD=2∶3∶4。如果AB的中点M和CD的中点N的距离是2.4cm，求AB，BC，CD的长度（如图2）。

分析：题设条件告诉我们3条线段AB，BC，CD长度的比值，这就是说，如果用一个适当的单位长度去度量，这3条线段的结果分别是：AB，BC，CD分别含有2个、3个、4个这样的长度单位。我们不妨设这个单位长度为k，则AB=2k，BC=3k，CD=4k图形问题就与数量问题紧密结合在一起，根据题设中M，N两点在图形中的位置，很容易求得MN与k的关系，从而求得k值。

解：A、B、C、D是直线l上的4点，且AB∶BC∶CD=2∶3∶4。

设AB=2k，那么BC=3k，CD=4k。

∵M是AB的中点，N是CD的中点。

即6k=2.4，

∴ k=0.4。

由此可得AB=0.8（cm），BC=1.2（cm），CD=1.6（cm）。