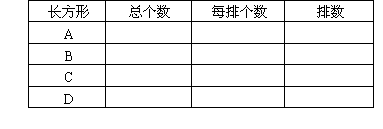
教学目标

(一)初步理解长方形面积计算公式的推导过程，能正确地计算长方形的面积．

(二)在长方形面积计算公式的推导过程中，培养学生抽象概括能力及动手操作和解决实际问题的能力．

(三)在教学中渗透辩证思想、函数概念等．

教学重点和难点

重点：理解并掌握长方形面积的计算公式，能正确地计算长方形的面积．

难点：引导学生通过亲身实践推导长方形面积的计算公式．

教学过程设计

(一)复习准备

启发谈话：

上节课我们学习了面积和面积单位，老师给同学们留了一道思考题．如果我们要测量学校的操场面积，用一平方米的面积单位，一个一个地拼摆，可行吗？

(不可行)今天我们来研究科学地计算方法．(板书课题：长方形面积的计算)

(二)学习新课

1．动手操作，弄清基本关系：

每排个数、排数与总个数的关系．

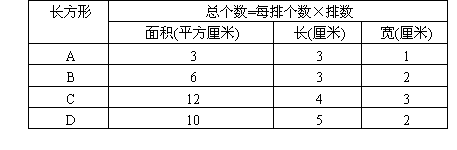
请同学拿出1平方厘米的小正方形，摆出上面的长方形想：一排摆了多少个小正方形？一共摆了几排？

(学生操作时，老师把表格画在黑板上)

(一排摆几个小正方形、摆了几排、一共摆了多少个小正方形，它的面积是多少，老师依次在表格中板书出来)

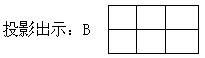
请同学用1平方厘米的小正方形摆出上面这个长方形．

每排摆了几个？摆了几排？一共有多少个？你是怎样算出来的？

(每排个数×排数=总个数)

前面讲过有多少个面积单位，面积就是多少．所以可以用“面积”代替“总个数”，在表格图“总个数”下面写上“面积”(平方厘米)．

下面就用简便方法计算长方形面积．

2．想象操作，弄清过渡关系：

长与每排个数、宽与排数的关系．

投影出示：C

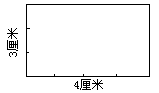
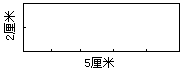
思考：这个长方形长4厘米，沿着长边，一排可以摆几个1平方厘米的正方形？

不用动手摆，脑子里想一想．如果长方形长5厘米、10厘米……一排可以摆几个呢？

那么，你发现了什么？(两个同学互相说一说)

生：长几厘米，每排就摆几个．

师：那么就是说，长可以代替“每排个数”老师在表格中“每排个数”下面写出“长”(厘米)．

再看，长方形的宽是3厘米，沿着宽可以摆这样的几排呢？

同学们不用动手摆，怎么知道可以摆3排呢？

能不能说出宽与排数的关系？

生：宽是几厘米，就可以摆成这样的几排．

师：那么，也就是说用“宽”可以代替“排数”．(老师在表格中，“排数”下面写上“宽”(厘米)．

请同学们很快求出这个长方形的面积是多少？说说你是怎样算出来的．

3．理解长方形的面积与长、宽的关系．

投影出示：D

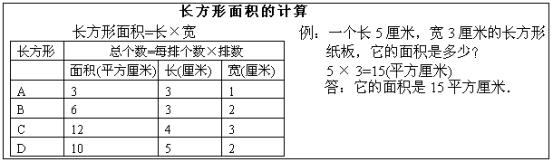
师：请同学们讨论一下，这个长方形的面积是多少？你是怎样求出来的？长方形的面积与它的长和宽有什么关系？

学生讨论后，老师引导学生对照表格，请仔细观察，再回忆一下，刚才的图A、图B、图C、图D．你发现了什么？

老师进一步引导学生，计算长方形面积的方法(最简单的)谁能概括出来？

学生总结归纳出：

长方形面积=长×宽(老师板书)

回顾一下，对照表格进行验证．

出示例题：

例：一个长5厘米，宽3厘米的长方形纸板，它的面积是多少？

师：用我们刚才学到的知识，请同学们自己解这道题．做完后，互相交换检查一下．

订正时，老师板书．

5×3=15(平方厘米)

答：它的面积是15平方厘米．

引导学生看书，质疑．

(三)巩固反馈

1．填表．(学生口答)

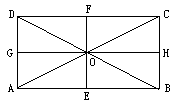
2．选择正确答案．

(1)一个长方形长6厘米，宽3厘米，面积是(　　　 )．

A．18厘米　　　　　　　　　　　　　　　　 B．18平方厘米

(2)一个长方形的长是8分米，宽是4分米，周长是(　　　 )

A．24分米　　　　　　　　　　　　　　　　 B．32平方分米

3．一个长方形花坛的面积是48平方米．问：它的长和宽分别可以是多少米？

长(米)　　　　　　　　 宽(米)　　　　　　　　　　　　 面积(平方米)

48　　　　　　　　　　　 1　　　　　　　　　　　　　　　 48

24　　　　　　　　　　　 2

16　　　　　　　　　　　 3

12　　　　　　　　　　　 4

8　　　　　　　　　　　　 6

小结 　这节课我们学习了什么？(长方形面积的计算．)要想求长方形的面积，必须知道什么条件？(长和宽)怎样计算长方形的面积？(长×宽=面积)计算长方形面积应该注意什么问题？(长和宽的单位名称要先统一)

小资料 〔长方形〕

两组对边分别平行且有一个角是直角的四边形，叫做长方形(也叫做矩形)．例如：下图是长方形ABCD．

长方形有如下的性质：

1．四个角都是直角，即∠DAB=∠ABC=∠BCD= ∠CDA=90°．

2．两组对边分别相等，即AB=CD，BC=AD．

3．对角线相等并相互平分，即AC=BD， AO=CO，BO=DO．

4．对角线的交点是长方形的对称中心．

5．每一组对边中点连线都是长方形的对称轴．即EF和GH都是它的对称轴．

一般把长方形中较长的一边叫做长，与长相邻的一边叫做宽．如果长和宽分别用a和b表示，那么，长方形的周长c=2(a＋b)，面积S=ab．

课堂教学设计说明

本节课是在学生了解了面积的意义，初步认识了面积单位，学会用面积单位直接量物体或平面图形的面积的基础上，进行教学的．通过调动学生的各种感观，亲自动手摆一摆，仔细观察，动脑筋想，从而推导出计算长方形面积的方法．在教案设计上，一步一步深入，从具体到抽象、从感性到理性．使学生自己悟出求长方形面积应该怎样计算．

巩固反馈练习的安排，考虑到对所学新知识的巩固、检查，又注意到新旧知识的联系．最后，根据本班学生的实际，安排了一道发散思维的练习，有利于激发学生的学习兴趣．

板书设计