如果有人告诉你，在任何6个人中，总可以找到3个相互认识的人或3个相互不认识的人(A认识B，B也认识A，就认为A、B是相互认识的)，你可能会将信将疑，但这的确是正确的，而且是近代组合学中著名的拉姆赛理论的特例，并被选为1947年～1951年匈牙利数学竞赛试题，成了有名的经典例子。

　　拉姆赛理论是英国数学家、哲学家兼经济学家拉姆赛1928年在他的一篇文章中提出的，它的核心内容是“任何一个足够大的结构中必定包含有一个给定大小的规则子结构”。

　　关于上述例子的证明是很有意思的：

　　6个人用6个顶点表示。两个人相互认识用实线相连，两个人相互不认识则用虚线相连。

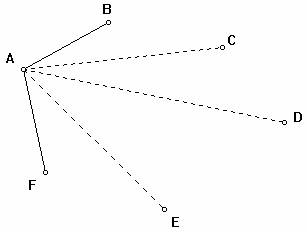
　　考虑A所连出的线，在5条线中每一条不是虚线就是实线，因此一定有一种线的数目≥3(这实际上用了抽屉原理)。不妨设AC、AD、AE是虚线，这时连线CD若是虚线，则C、D、E就是相互不认识的3个人，已经满足题目要求，因而设CD是实线。同理，CE、DE是虚线时也已经找到3个相互不认识的人，从而也只能是实线，但这时C、D、E成为相互认识的3个人，题目条件同样被满足。所以，无论如何总能找到3个相互认识或相互不认识的人。