 |
数一数有几个正方体 |
看着上面这个图,小光不以为然地说:“我一眼就能看出有5个正方体,这也算是问题?”
小光也沉不住气了:“让我看看,怎么回事?” 小兵说:“依我看,这个图形上面缺了一个角,正好把下过多余的一个正方体移过去补上.” 小光一看恍然大悟,原来是下边这个多余的正方体捣的乱,被它挡住的正方体现在露了出来.
立立看到同学们这么有兴趣,就出了一道难题,你能想出几种方法得出右图中小正方体的总个数呢? 这回小光胸有成竹地说:“我用拼补的方法,把最上面一层的2个正方体移动到中间一层,补上缺少的部分,原来的图形就转化成了一个长方体.数一数一层有6个正方体,那么2层就有12个正方体;我还可以用计算的方法,l列2个,3列是3个2个,2乘 3得 6,这是一层的个数;一共有2层,就是 2个6,6乘2得12,这是两层一共有小正方体的总个数.” 方方说:“我再来补充一种方法,把原图形象这样分开,左边图形的小正方体个数是1+2+3=6,求2个同样图形的小正方体个数是6×2到12.” 小强说:“我明白了,不管用拼补转化的方法,还是分解图形的方法,目的都是为了便于观察和更好地通过计算解决问题.” |

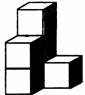
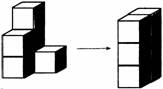 方方拿过5个正方体就摆了起来,可奇怪的是她怎么也摆不出同样的图形,急得她大喊:“你们快来帮忙呀!”
方方拿过5个正方体就摆了起来,可奇怪的是她怎么也摆不出同样的图形,急得她大喊:“你们快来帮忙呀!” 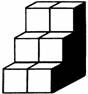 小红高兴地说:“现在好数啦,l行有2个,3行就有3个2个,2乘3得6;1列有3个,2列有2个3个,3乘2也得6.”
小红高兴地说:“现在好数啦,l行有2个,3行就有3个2个,2乘3得6;1列有3个,2列有2个3个,3乘2也得6.”